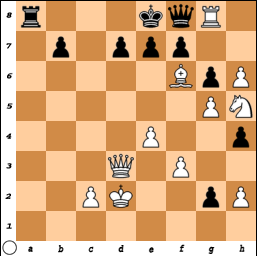
Kan wit mat geven in twee?

Wellicht, maar dan zullen we eerst moeten vaststellen of zwart nog mag rokeren.

We kunnen zien dat de pion op g2 moet gekomen zijn van c7 en daarvoor moet deze ten minste vier keer hebben geslagen.  Toch?

Dus komt de pion op g6 van g7 en de pion van h4 van h7 want, indien g6 van h7 en h4 van g7 zou komen, zou er nog eens twee keer geslagen moeten zijn en dat is één keer te veel omdat wit nu eenmaal niet meer dan vijf stukken mist.

Dát betekend dat zwarts laatste zet niet kan zijn h7 x g6. Duidelijk?

We gaan verder.

Wat zou zwarts laatste zet kunnen zijn indien we er van uit gaan dat dit niet met de koning en eveneens niet met de toren op a8 is geweest omdat in dát geval zwart sowieso niet meer kan rokeren.

Daar blijven dan vooralsnog vier mogelijkheden over.

1: Dame van g7 – f8 (wat betekend dat wit de zet ervoor met de toren een zwart stuk zou hebben moeten geslagen en zwart schaak heeft gegeven.  Immers kan de toren alleen van h8 naar g7 zijn gegaan door te slaan en tegelijkertijd schaak te geven waardoor de dame van g7 naar f8 gaat.

2  :  g7 – g6

3:    Dame g7 x f8, dus de dame slaat een wit stuk.

4:    g3-g2

Andere zetten zijn niet mogelijk.

Alvorens deze vier mogelijkheden nader te onderzoeken kijken we naar wat overige zaken.

Eén van de vier witte pionnen, e4, f3, g5 en h6 moet gekomen zijn van d2 en tezamen heeft dit pionnencollectief vier keer geslagen.

Het vijfde (óf misschien het zesde, daarover later) missende stuk is geslagen op c8 en wel de loper vanwege de aanwezigheid van de pionnen b- en d7.

Hieruit volgt dat géén van de reeds missende twee pionnen van a2 en b2 samen nooit meer dan één keer hebben geslagen.

Wit mist deze twee pionnen en nog eens drie stukken.

Vier witte stukken werden door de pion geslagen op weg van c7 naar g2

De pionnen a2 en b2 kunnen niet geslagen zijn door deze zwarte pion want zelfs de pion van b2 moet minstens twee keer geslagen hebben wil deze de d-lijn kunnen bereiken en we “bewezen”zonet dat ze maar maximaal één keer kan hebben geslagen.

Volgt u ’t nog?

Oké.

Daarom moet ten minste één van deze twee pionnen zijn gepromoveerd (anders kan de pion van c6 naar g2 nooit vier keer hebben geslagen).

Onthouden we thans twee zaken:  de pionnen van a2 en b2 hebben samen nooit meer dan één keer stuk geslagen en ten minste één van deze is gepromoveerd.

Met dit in het achterhoofd keren we terug naar de vier mogelijkheden voor zwarts laatste zet.

Bekijken we eerst misschien wel de eenvoudigste, mogelijkheid 1. Wit moet dan met de toren eerst een zwart stuk hebben geslagen wat inhoud dat, indien dit stuk daar geslagen was, de pionnen van a2 en b2 niets geslagen kunnen hebben.

Zo ook ons tweede optie:  indien de laatste zet van zwart g7-g6 is, en indien we weten dat de zwarte loper van c8 op c8 geslagen moet zijn, en de pionnen e2, f3, g5 en h6 vier keer hebben geslagen moeten we concluderen dat de pionnen a2 en b2 niets hebben geslagen.

Met andere woorden: a2 én b2 zouden niets hebben geslagen, maar wel, om genoeg stukken voor zwart te hebben om te slaan, moet één van deze twee pionnen zijn gepromoveerd en dat kan, in dit geval, alleen op veld a8 wat betekend dat met de toren,  thans op a8, minstens twee zetten is gedaan.

In het derde geval:  De dame slaat een stuk op f8.  Dan moeten de twee beide pionnen zijn gepromoveerd om voldoende stukken te hebben die volgens de stelling geslagen zouden zijn. En daarbij komt, dat de pion van c7 naar g3 alles geslagen heeft op de zwarte velden en dus de witveldige loper van wit door een ander stuk of pion elders werd geslagen.

In deze twee gevallen heeft alleen de pion b2 op zijn weg naar promotie geslagen (om veld c6 te bereiken) en moet er wederom minstens twee zetten met de toren zijn gedaan om de pion van a2 te laten promoveren.

Ergo: zwart kan niet meer rokeren.  Dus kan wit mat in twee geven.

En dat moet voor de lezers alhier toch een eitje zijn.

De componist hiervan is Raymond Smullyan 1919 – 2017 en dit is één van zijn 50 schaakpuzzels uit The chess mysteries of Sherlock Holmes, 1979, ISBN 0394737571, een boek dat elke zichzelf respecterende schaakverslaafde in zijn schaakboekenkast zou moeten hebben staan.

Willem