Soms kom je de mooiste problemen tegen, al is, op zich genomen, dat al een paradoxale tegenstelling.
En één van de mooiste vertel ik thans met eigen woorden. Mooi omdat er meerdere mogelijkheden zijn waarom er een bepaalde zet helemaal niet gespeeld kan worden.
Onlangs liep ik met een bekende schaakmeester een grote, statige kamer binnen waar juist twee amateurschakers die wij beide kenden een partij aan het schaken waren en daarbij zag de schaakmeester nog net dat de witspeler een zet deed met de nog in het spel zijnde loper; zelf zag ik dat het geen grote talenten waren, want de partij was dusdanig dat de speler met de zwarte stukken, zo te zien, al lang had moeten opgeven. Hij stond immers totaal verloren.
De twee spelers stonden op; de ene schonk wat te drinken voor ons in terwijl de andere uit een oude oma-kast wat versnaperingen opduikelde en deze naast het schaakbord op tafel zette en ondertussen voerden we gevieren een oppervlakkig nietszeggend gesprek waarvan ik inzake de inhoud mij niets meer herinner dan alleen dat het weer eens over schaken ging.
Na enige minuten namen beide spelers weer plaats achter het schaakbord en meteen wilde zwart zijn volgende zet doen; zijn linker hand ging al naar de toren en zijn rechter neigde naar de koning teneinde een rokade uit te gaan voeren. Op dat moment boog de schaakmeester zich naar de zwartspeler toe en sprak met enige stemverheffing: “Ho ho; je mag helemaal niet rokeren!!
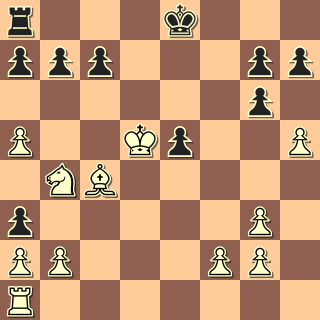
Dit was de stand……
We gaan stap voor stap; en wederom stel ik weer chocoladeschaakstukken ter beschikking; drie keer, voor elke oplossing weer één….


Die meester telt dan sneller dan ik 😉
Ja, het is ook een uiterst geniale meester… Maar WAAROM weten slechts alleen de spelers…. Dat maakt het juist zo interessant…
Lastig hoor Willem
Maar ik denk dat ik er wel uit ben
I: alle zwarte stukken die van het bord zijn verdwenen zijn geslagen door witte pionnen (hxg3, e2x..xh5, cxbxa)
II: alle witte stukken die van het bord zijn verdwenen zijn geslagen door zwarte pionnen (fxg6, dxcxbxa3), behalve de witte d-pion natuurlijk
De zwartveldige witte loper is geslagen door de zwarte d-pion die nu op a3 is beland, vanwege II.
Dat betekent dat de laatste zet met die pion b4xa3 is geweest. Dus a4-a3 was niet de laatste zet.
e6-e5 was ook niet de laatste zet, vanwege schaak. Immers de laatste witte zet was een loperzet.
e7-e5 was ook niet de laatste zet, want dan kon de zwarte loper van f8 nooit spelen, en dat is in tegenspraak met I
f7xg6 was ook niet de laatste zet, want dan kon de zwarte toren van h8 nooit spelen, en dat is in tegenspraak met I
Dus de laatste zet van zwart was of met de koning of met de toren. Dus mag er niet gerokeerd worden
verder mag je natuurlijk niet met twee handen rokeren, maar dat terzijde
Aardig op weg Abe. Om er maar eentje te noemen: f7 x g6 kan best de laatste zet zijn geweest…
Inderdaad: de pion op g3 heeft één slagzet gedaan, de pion op h5 3 en de pion op 5 twee, tezamen 6. Alle zwarte stukken moeten wel geslagen zijn door de witte pionnen. De zwarte “h8” toren kan wel degelijk eerder zijn geslagen, maar daarvoor moet de koning eerst plaats maken (wat betekend dat er geen rokade meer mogelijk is) om hem er uit te laten. Zo kan de toren op de laatste zet van zwart door f7 x g6 zijn geslagen.
Met andere woorden: de laatste zet van zwart hoeft dus niet, zoals jij schrijft, met toren of koning zijn gedaan, maar kan ook f7 x g6 zijn. Of wellicht een andere?
Dat maakt het probleem zo mooi….
Inderdaad, duidelijk, wanneer de laatste zet met de koning of toren was, kan er niet worden gerokeerd. Ook dus, zoals we zagen, als de laatste zet f7 x g6 was, kan er niet worden gerokeerd vanwege het feit dat dan de koning plaats heeft moeten maken om de toren doorgang te verlenen.
Maar dan:
De zwarte pion op a3 heeft drie of vier slagzetten gedaan, afhankelijk vanaf het veld waar hij van komt. als hij komt van d7 drie, als hij komt van e7, vier keer slaan…
Zoals we reeds zagen, de pion op g6 maakte één slagzet.Dan zijn dus totaal ten minste vier van de vijf witte stukken die reeds van het bord verdwenen.zijn door die pionnen geslagen.
Dat zou betekenen dat de pion op e5 geen twee stukken heeft geslagen.
Dat wil weer zeggen dat de pion op e5 niet met een slagzet vanaf f6 komt.
Aan de andere kant: als de pion van d6 komt, en hij kwam ook al eerder van e7, dan maakte hij twee slagzetten, of , anders kwam ze van d7, in welk geval a3 moet zijn gekomen van e7 in plaats van d7, samen zes slagzetten, inclusief de slagzet op g6, wat één teveel is.
Daarvoor: wanneer e5 de laatste zwarte zet zou zijn, kan de pion niet komen van e6 omdat de laatste zet van wit met de loper was. en inderdaad, komt de pion van e7, dan zou de zwarte c- loper niet door een witte pion zijn geslagen…
Laten we vervolgens kijken naar de zet a4-a3.
naast f7xg6, een andere mogelijke zet..
Wanneer de pion op a3 komt van a4, kan het niet anders of hij komt van d7, en dan slaat hij drie keer. En wat dan opvalt, alle drie op de witte velden. Ook de zet f7xg6 slaat een wit veld.
Vier van de vijf witte stukken zijn dus geslagen op een wit veld.
De witte c1-loper, echter, moet geslagen zijn op een zwart veld.Dus niet door één van de pionnen. De enige mogelijkheid zou dan kunnen zijn dat de pion afkomstig van d2 ook geslagen is op een wit veld.
Maar hier rijst een nieuw probleem.
Om zich te laten slaan zou het eerst (door slag) de d-lijn moeten verlaten en dat is weer niet mogelijk omdat alle zwarte stukken die van het bord verdwenen door de pionnen a5, g3 en h5.
Dit betekend dat de d-pion van wit eerst naar d8 is gewandeld waardoor op enig moment de koning met schaak even heeft moeten plaats maken en ja, dan is rokade al niet meer mogelijk. Vervolgens zou dit stuk zich weer hebben aangeboden op een wit veld om alsnog door een zwarte pion op een wit veld geslagen te worden.
Kortom: in tegenstelling tot hetgeen Abe concludeerde, zijn er zijn dus vier laatste zetten mogelijk; met de koning, met de toren, f7xg6 of a3-a4 en alle vier de zetten hebben hun eigen oorzaak waarom rokade niet meer mogelijk is.
Dat zag de meester in één oogopslag, maar wélke zet, dat konden allen de spelers zelf weten en dát wist de meester natuurlijk niet.
Overigens: dit was weer een uiterst mooi probleem gecomponeerd door Raymond Smullyan rond 1979, met allerlei subtiele en weergaloze wendingen.
Inderdaad, nummer 9 uit “mijn” boek!
het is nu ook Willem “zijn” boek 🙂