Wat ziet de schaakmeester in één oogopslag wat wij niet zien?
Soms kom je de mooiste problemen tegen, al is, op zich genomen, dat al een paradoxale tegenstelling.
En één van de mooiste vertel ik thans met eigen woorden. Mooi omdat er meerdere mogelijkheden zijn waarom er een bepaalde zet helemaal niet gespeeld kan worden.
Onlangs liep ik met een bekende schaakmeester een grote, statige kamer binnen waar juist twee amateurschakers die wij beide kenden een partij aan het schaken waren en daarbij zag de schaakmeester nog net dat de witspeler een zet deed met de nog in het spel zijnde loper; zelf zag ik dat het geen grote talenten waren, want de partij was dusdanig dat de speler met de zwarte stukken, zo te zien, al lang had moeten opgeven. Hij stond immers totaal verloren.
De twee spelers stonden op; de ene schonk wat te drinken voor ons in terwijl de andere uit een oude oma-kast wat versnaperingen opduikelde en deze naast het schaakbord op tafel zette en ondertussen voerden we gevieren een oppervlakkig nietszeggend gesprek waarvan ik inzake de inhoud mij niets meer herinner dan alleen dat het weer eens over schaken ging.
Na enige minuten namen beide spelers weer plaats achter het schaakbord en meteen wilde zwart zijn volgende zet doen; zijn linker hand ging al naar de toren en zijn rechter neigde naar de koning teneinde een rokade uit te gaan voeren. Op dat moment boog de schaakmeester zich naar de zwartspeler toe en sprak met enige stemverheffing: “Ho ho; je mag helemaal niet rokeren!!
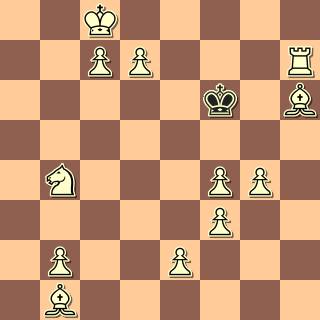
Dit was de stand……
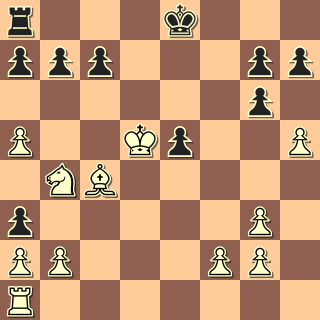
We gaan stap voor stap; en wederom stel ik weer chocoladeschaakstukken ter beschikking; drie keer, voor elke oplossing weer één….
Twee oplossingen?
Twee oplossingen, maar weer is er slechts één de juiste.
Dus is er maar één goed.
Waarom?
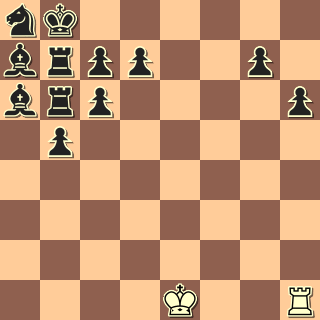
Maar dan heb je het toch echt mis!!
Wit geeft hier mat in twee; als je er al achter komt hoe, denk je dat er twee mogelijkheden zijn. Echter: er is er maar één!
En dan: hoe luidt de oplossing. En onderbouw dit met echte onvervalste schaakargumenten.
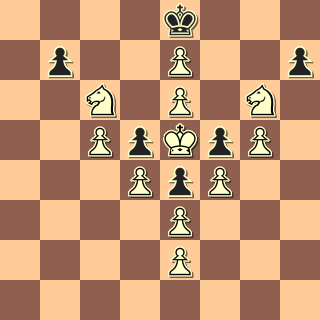
..en ook niet zo moeilijk....
De vorige opgave had kennelijk wat moeilijkheden; slechts één oplosser vond de vier matten en kan zijn chocoladestukken tegemoet zien.
Daarom dit keer eentje waar je gewoon even niet hoeft te matten, juist niet…
Wit aan zet en geeft GEEN mat in één…..
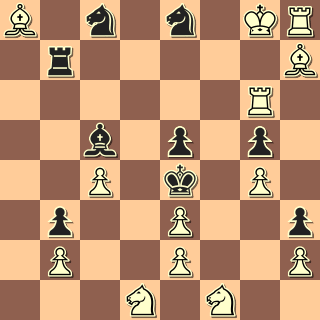
98 jaar oud, maar toch...
Wit geeft vier keer mat in twee….
Om even te bezigen….
1: Geef in deze stelling mat in twee
2: draai het bord een kwart slag en geef wederom mat in twee
3: draai het bord wéér een kwart slag en geef nogmaals mat in twee,…
En om het af te maken:
4: draai het bord wederom een kwart slag en geef nog een laatste keer mat in twee.
Voor de eerste goede oplossing van de vier matten stel ik een zakje chocoladeschaakstukken beschikbaar….
Een vreemde tweezet
Welaan, voor de echte liefhebber.
Wit geeft mat in twee zetten. Dat kan helemaal niet, dus doen we er voor dit keer één spelregel bij. Wit mag promoveren tot elk stuk wat hij maar wil.
Dat was voor mij zelfs te gortig
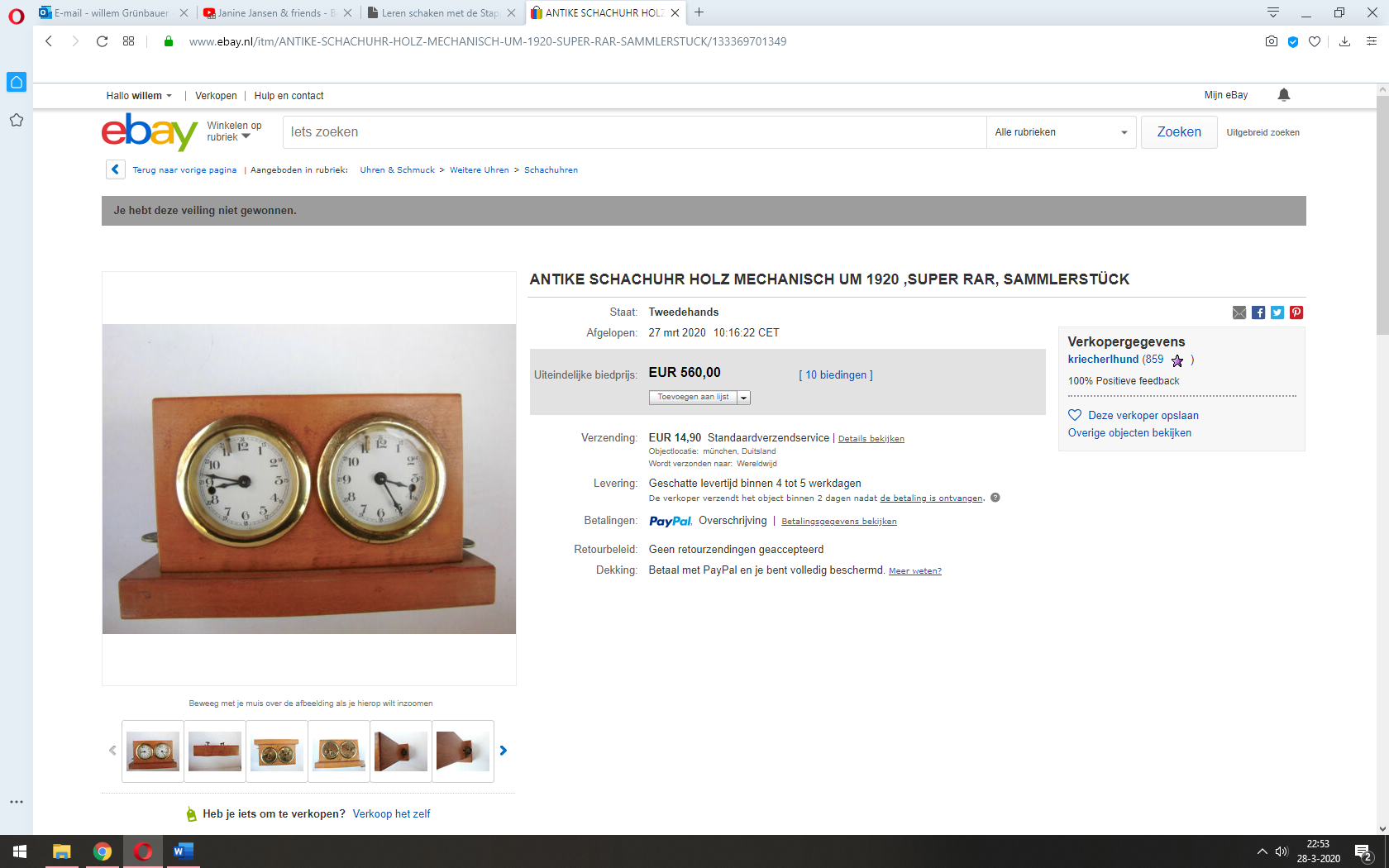
Wellicht is het jullie bekend dat ik er een schaakklokkenverzameling op na houd. Nu zag ik op EBAY een leuk klokje voorbij komen waarbij in de “bediening” twee oude munten waren verwerkt.
Natuurlijk deed ik er een bod op, maar anderen zagen er meer waarde in dan dat ik er voor wilde geven.
560 euro voor een klokje, daarmee tikte dit klokje wel een heel erg hoge rating aan….
Maar Abe weet vast wel weer welke deel van het stappenplan moet worden geraadpleegd.
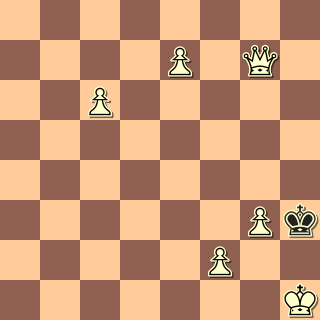
Het ziet er hier maar remiseachtig uit, niet waar? Al is zwart hier aan zet.
Maar hier zit weer wel een opdrachtje aan vast om het komende weekeinde over na te denken. ditmaal gewoon, met de huidige spelregels. Niks gekkigheid of onzin
Wit neemt zijn zet terug en daarna zwart eveneens….
Daarna doet zwart een andere zet en dan geeft wit meteen mat in één. Hoe zou dit dan moeten gebeuren?











